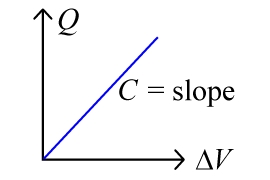Capacitance is the ratio of the magnitude of the charge on one plate of a capacitor, Q across an object, to the potential difference across the capacitor, ΔV.
Eric Murray, Fall 2006
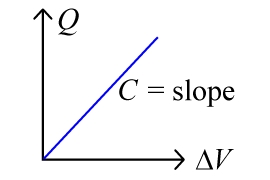Capacitance is the ratio of the magnitude of the charge on one plate of a capacitor, Q across an object, to the potential difference across the capacitor, ΔV.
C = Q/ΔV
The charge on a capacitor can be determined by integrating the current up to time when ΔV is measured.
Q = ∫I dt
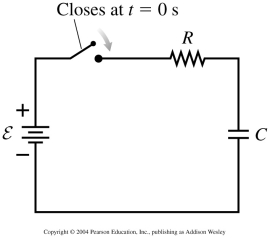When a constant electric potential difference is suddenly applied across a circuit consisting of a capacitor and a resistor in series, the potential difference across the capacitor, ΔVC, the potential difference across the resistor, ΔVR, and the current in the circuit, I, all vary with time, t. There is a characteristic time, τ, called the time constant. For example, the current varies with time according to
I = I0e-t/τ
where I0 is the current at time t = 0, the instant the switch is closed.
To determine τ, you will fit the current vs. time graph to a general exponential decay curve,
I = Ae-Bt + y0
where A, B, and y0 here are fit parameters. The fit parameter B is related to the time constant by τ = 1/B, while the capacitance C is related to the time constant by τ = RC.
Fitting a general exponential decay curve will provide not only the fit parameters A, B, and y0, but also their experimental uncertainties, ΔA, ΔB, and Δy0. Finding the time constant from the fit parameter using τ = 1/B is straightforward, but Δτ is not ΔB. (For one thing, Δτ and ΔB have different units.)
If we had multiple measurements of τ, we could calculate an average and standard error, and report the standard error as the experimental uncertainty in the average. On the other hand, sometimes it is necessary to calculate an experimental uncertainty from the uncertainty in one or more measured parameters.
In general, if a calculated result y is a function of measured parameters x1, x2, …, xn, each of which has an uncertainty Δx1, Δx2, …, Δxn, then the uncertainty in y can be calculated by
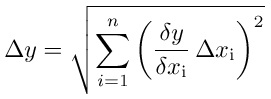
where δy/δxi is the partial derivative of y with respect to xi. (Partial derivatives, if you have not encountered them, are even easier to find than regular
derivatives, because you pretend that everything, other than the parameter you are taking the derivative with respect to, in this case xi, is a constant.) This is the error propagation
formula, and it is assumed that the uncertainties in all the measured parameters xi are independent.
Consider, for example, calculating the electric potential due to a point charge from measured values of Q ± ΔQ and r ± Δr. The potential with respect to zero at infinity would be found using V = kQ/r. The uncertainty in V (not to be confused with a potential difference despite being expressed as ΔV) is
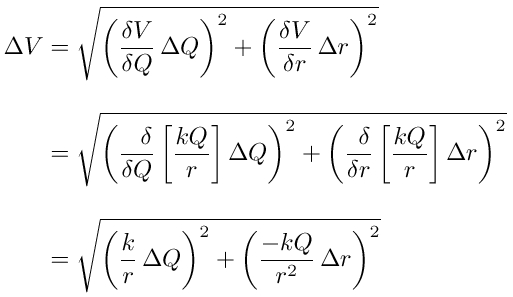
You should now be able to find the relationship between the uncertainty in the time constant, Δτ, and the uncertainty in the fit parameter, ΔB. Find the relationship, and come to lab prepared with it.