Lab Practice; Error Bars, etc.
You are encouraged to read and digest the following notes which are applicable to all
(or many) of the labs. In grading reports we will be requiring you to follows these
practical matters. The various components here are:
A. Entering numerical results on lab report sheets.
B. Accuracy Limits. Estimates of "Error".
C. Curve fitting
D. What to do about "wrong" data points.
E. Care of Equipment
A. Entering numerical results on the Lab report sheets.
Frequently you will be required to enter a numerical result in a "block" on the report sheet. The blocks generally will allow for up to 7 digits of information; often we have written after the block the units in which we would like you to quote the answer.
Suppose that you have concluded that the numerical result that you need to enter is 1340.0 Amps. Look first at the units we have written following the block. Let us suppose these are "mA" meaning milliamps (or units of 10-3 Amps). Now 1340.0 amps is equal to 1340000.0 ma. That will not fit a 7 digit block. An alternative and completely acceptable way of writing the answer in the block will be 1.34e+6 ; this will fit in the box and will be properly in units of mA and represent 1.34 x 10+6 mA.
A word or two of caution. If we have provided a box with units of mA then it probably means that we expect an answer of a few mA and we do NOT expect an answer of millions of milliamps. So if the magnitude of your answer seems greatly different from the magnitude we have designed for the "box" then it probably means that you have got it wrong and you should rethink your results and check that you have the decimal point in the right place. In the example given a current of 1340.0 Amps is really huge, will never be seen in our labs, and probably represents more than the total current into the Physics building at its busiest time.
You might also be tempted to give a long string of numbers which will not (apparently) fit the box. For example you might want to give an answer of 1342.9876 amps. That implies an "accuracy" of 8 significant figures. We never in this lab (or probably any other educational lab you will ever experience) get such an accuracy. Generally the accuracy is not better than 3 significant figures which means it makes no sense to quote this answer in 8 figures and the only sensible answer to quote is a value rounded to 3 figures or 1340 amps (or 1.34 10+3 Amps or 1.34 x 10+6 mA. So if you are trying to fit a number into our boxes and it will not go then you are probably quoting a result with an accuracy which is not justified and you should think again. The question of accuracy limits is discussed in section B below.
B. Accuracy limits. Estimates of "Error".
No physical (or engineering) measurement is ever "completely" accurate. There is always some uncertainty. There are three types of "limitation" to the accuracy. To be specific lets consider measuring the distance from Atlanta to Chattanooga by driving in a car and reading distance on the odometer. For a start there is a "least count" limit; the distance measuring device in a car only read to 0.1 miles on the last digit. So we have no information about the distance measurement in the second or third decimal place. Secondly there is always some possible error in setting up the measurement. If we drive around the outer curves on the Expressway we will get a slightly longer distance than if we drive around the inner curves. And where is the end of the trip anyway? At the Chattanooga choo-choo or at the City Hall or somewhere else? Each time we try the measurement then we are likely to get a slightly different result. We would consider these to be "random" experimental errors. Then, finally, the odometer might be plain wrong (the odometer assumes that the circumference of the tire is like the new one supplied with the car; if your tire is worn then this is wrong, or if you have put on larger diameter tires it is wrong). This would be called a "systematic" error.
To be specific we will use as an example the measurement of a distance between two knots on a piece of string separated by about one and a half meters, and to do this we are using a 10 meter long tape measure (or ruler). The meter rule will have divisions marked on it at meters, centimeters, and millimeters.
Least count limit:
You lay the string next to the ruler with one knot at the zero end and look at the position of the second knot. Suppose the second knot lies somewhere between the mark at 1 meter, 53 centimeters, 6 mm and the next mark at 1 meter, 53 centimeters and 7 mm. What can you say about the length between the knots? Well it is certainly between 1.536 and 1.537 meters. If you are very careful you might be able to judge the location of the knot between the two millimeter marks and maybe its about 6/10 of the way along and so you could conclude that the length between the knots is 1.5366 m. That is absolutely the best you can do with this technique. That is a five figure accuracy and the equipment will not allow you to do any better. So our first conclusion is that there is not justification at all for quoting an answer which has more than four decimal places for this case. This is a sort of a "least count" limitation. With any instrumentation there is a last digit beyond which the equipment will not record or measure. There is absolutely no justification for giving an answer which implies an accuracy better than this last figure given by the instrumentation. We can write an answer 1.5366 m. We cannot decide whether the true answer is 1.5366555 or 1.53663333 because the equipment is not good enough. Never quote an answer to more figures than the instrument will record.
Random Errors.
Repeat the measurement a number of times starting from scratch each time. Lay the string out again with one end at the zero and find the position of the other end. It is likely that each independent attempt will give you a slightly different answer. Suppose that five trials give you 1.5366, 1.5351, 1.5375, 1.5380, 1.5355 meters. Why should they be different? Well there are a number of practical problems or limitations. The knots have a size (probably about one millimeter) and it is difficult to decide exactly when the knot is at the zero and where the other knot lies. Each time you try the measurement the answer will be a bit different due to the difficulty of deciding where the knots might lie against the ruler. Also it is possible that the string sags or stretches differently each time giving you again a different result. What can one conclude about the "true" length? Well the best thing to do is to repeat the measurement (like the five times) and take an average. The average of the five data points given in this example is 1.53654(+maybe additional numbers depending on the setting of your calculator). Is this what you should quote? Now we already decided that the "least count" accuracy of the meter rule is a tenth of a mm so we can only legitimately claim a four decimal point accuracy and so we should "round" the number to four decimal points and get 1.5365 m.
So is the figure 1.5365 meters all we should quote?? Not really. The individual measurements have ranged from a lowest value of 1.5351 to a high of 1.5380 ( a difference of 3 mm or roughly 1.5 mm to either side of the mean) and we can use this "variation from the mean" to indicate to the reader how reproducible the measurements were. We can indicate the extent of the variation by quoting the answer as being the mean value of our measurement and + or - the variation from the mean. That gives us 1.5351 +/- 0.0015 m, which we could also write as 1.5351 +/- 0.1%. The accuracy limit would then be +/- 0.1% (there is no point in writing accuracy estimates to much more than a one or two significant figures--these are only estimates to give an indication of reliability).
This method for estimating accuracy (as the percentage variation from the mean of a group of independent measurements) will be acceptable in this lab.
A detailed theory or "random errors" shows that if you make a large number of (truly) independent attempts and plot a histogram of the results then you find they approach a Bell shaped distribution. A more professional way of estimating an "accuracy" for a Bell shaped distribution is to take the differences of the individual measurements from the mean value and then calculate the root of the mean of the squares of these differences; then use that as the estimate of accuracy. It takes a bit of effort; you can use this if you prefer but its not really justifiable if the number of independent attempts is low, like five.
At the end of it all rethink whether the final quoted result of 1.5351 +/- 0.0015 makes any sense. First are the number of significant figures reasonable? Yes. We argued that we can "judge" a distance of 1/10 th mm and we quote an answer where the last digit is 1/10 mm . The quoted reliability is +/- 1.5 mm. We could have the positions misjudged by a about the size of a knot and the knots are about 1 mm in size and the quote reliability is about 1.5 mm or about the size of a knot; so this all makes sense.
Result! We can quote an answer of 1.5351 m and say that the reproducibility of the measurement is +/- 0.1%.
Systematic Errors.
How good is the meter rule? If it is made of metal it will expand on a hot day and contract on a cold one. If it is made of wood then it will also change length depending on humidity (gets longer on a wet day). Also the manufacturer will have had a "tolerance" in mind when the ruler was manufactured. How good was the equipment which printed the scales? Generally a manufacturer of an instrument will quote to you an accuracy of that instrument for use under normal conditions. For the case of the ruler the manufacturer might say that, for normal temperatures and humidity, and taking into account the accuracy of his equipment, the ruler is accurate to only 1%. This means the one meter marking on the rule may in fact be as much as 1.01 meters from the zero or as little as 0.99 m from the zero. This leads to a "systematic error". If the meter rule is too "long" by one percent then everything you have measured will be too short by one percent (and likewise if it is too short). Working out the systematic error requires knowledge of manufacturers specifications; we will not bother with it in this course but for most of the electronic measurement equipment the equipment has less than a 5% systematic error.
What should you quote for these labs?
In a professional situation you should give a complete quotation of all you know about the measurement. Going back to the knots on the string the answer we could reasonably quote would be: "The distance between the knots is 1.5351 meters with a random error (or reliability) of +/- 0.1 % and with a possible systematic error of +/- 1%".
In this lab we will be a little less ambitious.
- If we ask only for a single data point to be quoted then give an answer which is consistent with the number of digits provided by the instrument you are using.
- If we ask you to repeat the measurement a number of times then quote the mean of the measurements and give an accuracy limitation based on the spread of these points from the mean.
- Think about systematic errors. You may want to include them as part of your discussion.
C. "Curve Fitting"
In some of the experiments you will need to "fit" a mathematical model to some data points to extract some relevant values. This can be done automatically with "fitting programs" found either in the operating system of the PASCO software used (in some experiments) for data collection or in the EXCEL spreadsheet software. This needs to be done with some care and thought; we will illustrate this with an example.
Suppose you are measuring the voltage across an inductor when it is connected via resistor to a battery (this is relevant to experiment #6 and with different symbols also to experiment #3). The theory says that the equation for the voltage should be
V =
exp (-Rt/L) (1)
You acquire a bunch of data points for voltage V (volts) at various times t (seconds). The software will have a "fitting program" which fits to your data the equation
Y = a1 + a2 exp (a3 x + a4 ). (2)
So the values of Y will be the voltage V and the values of x will be the time t.
First what do we mean by "fitting" The program takes Eq #2, chooses some values of the coefficients "a", calculates Y at various x (or V at various times t) compares this with the data points, measures the divergence of the data points from the predictions and then repeats this for different values of a until the divergence of the data points from the predicted curves is a minimum. Then it stops and gives you the values of the coefficients "a" which represent the best fit (or least divergence from the data points). Also it will plot the line of Y (representing voltage) as a function of x (representing time) on your graph for you to make a visual comparison with the data points. It may also give you a "figure of merit" (often called Chi) which represents how good the "fit" is and represent the remaining deviation of the points from the predicted curve.
What should you do with all this? First look at the plot. If the plotted line seems to agree pretty much with your data points then you can continue. If it disagrees with the data points then you need worry about why; the fit is no good and there is no point in using the coefficients a. We will discuss reasons for "very bad" fits later.
So the fit is good and you have available the coefficients a. First thing is to compare the two equations (1) [what you expected] and (2) [the fit curve]. They are obviously (a bit) different. The theoretical equation (1) has no term like a1 or a4 in it. So we really expect these to be zero. If all the data points were of "total" accuracy then these fitted values of the two coefficients should have come out to be zero. In practice all data points have some "limitations" on their accuracy so they are not quite where you expect and the fitting procedure may give you non-zero values of these coefficients. First thing is that the fitted values of these two coefficients should be small (because in theory they should be zero); second thing is that if you were to set them to zero then it should make little difference. The available programs allow you to set those coefficients to anything you like. So set each of a1 and a4 to zero. The fit is repeated and now we have fitted the equation
Y = + a2 exp (a3 x ). (3)
The values given by the software for a2 is the value of ; the value given
for a3 is -R/L. The graph will now look something like
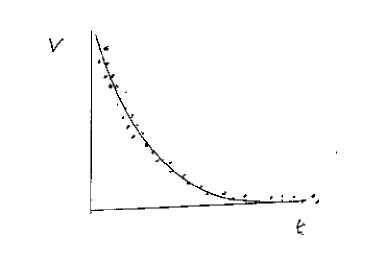Fig. 1 Exponential Plot
With luck that is the end of your problem and you have the result you need.
Bad Fits??
If the "fitted" line looks does not agree with the data points then what’s up? If the plotted "line of best fit" disagrees with your data points (particularly if it is very badly different) then you have made a mistake and you need to correct things. There is no point in using the data till you have fixed things. Generally speaking you should look carefully at the equation you are trying to fit and make sure that all the data on the screen are supposed to be given by that equation. If you have things on the screen which are NOT part of the equation then there is no way you will ever get a fit.
What to worry about?
(1) Your display may have various types of data on it and not all of these ought to be represented by the fitting equation. For example we will do experiments where you might end up recording two exponential decays on the graph. The fitting program will treat them like one. You may have a set of data which shows nothing for a while and then turns on to a high value followed by an exponential decay. The program will treat all the data (including the region where the apparatus is turned off) as all being part of the exponential decay. All of these problems crop up in the automatic data recording activities. Look at what you have got and select only the part of the trace which is supposed to be represented by the fitting equation; then try again.
(2) You may have one data point wildly off, like by factors of ten. Look for this on the plot; either discard the point or take another data set (happens particularly when students enter values by hand--they may put a decimal point in the wrong place)
(3) Sometimes when recording data automatically the first few points are "bad" due to (say) switching on or off of something. Select only points which are away from the start of the plot and try again.
(4) Sometimes the fitting routine can get plain "confused" and cannot "home in" on a good set of values. You can help matters by making a good "guess" as to the value of one of the coefficients and fix that and repeat the fit. If that looks better keep on repeating this until the fit is good. This happens particularly when you have only got a small number of data points (e.g. you cannot make a sensible fit to an exponential decay equation if there are only two or three data points in the changing part of the plot); you might be better off repeating the experiment with different settings and recording more data points.
(5) Sometimes the fitting routine insists on giving a large value to a coefficient which your theory says should be zero. This may mean your theory (or possibly the experimental configuration) is wrong. Check things and perhaps consult with the TA.
D. What to do about "wrong" data points.
What should you do about a data point which "looks wrong"? For example, you are measuring the distance between the knots in B above and you write down a distance of 1.435 meters which is about 10 cm different from all the other data. That point is clearly "wrong", no way you can get a length which is about one and a half meters "wrong" by ten cm, this probably was a personal slip, and one can throw it away.
If you are plotting a set of data points, y against x, and you expect a straight line and one data point is "off the line" what should one do about it? You should probably go back and repeat it a number of times. If all the measurements are "off the line" then you should worry about why this is true; you may have discovered something exciting!! [A number of Nobel prizes have been won by people who find a data point which is "off" the predicted line and which represent something nobody else has thought about.] If all the extra data points are pretty much "on the line" then you can probably throw out the first one as being an aberration.
In good scientific/engineering practice one should probably take very large numbers of measurements and use the average values of all of them (and throw nothing away). Then if there are one or two which are "off" for any reason then they will have little effect on the average. In the present lab there will probably not be enough time for such things.
E. Care of Equipment.
Leave the equipment the way you would expect to find it: neat and tidy. If there is something missing or something is not working then tell the TA as soon as possible. Things go wrong--we need to know about them so we can fix them.